El conjunto de los números reales pertenece en matemáticas
a la recta numérica que comprende a los números racionales y a los números
irracionales. Esto quiere decir que incluyen a todos los números positivos y
negativos, el símbolo cero, y a los números que no pueden ser expresados
mediante fracciones de dos enteros que tengan como denominador a números no
nulos (excluye al denominador cero).
Los números reales se representa con la letra


Existen tres maneras de expresar conjuntos mediante los números
reales.
1. Diagrama de venn
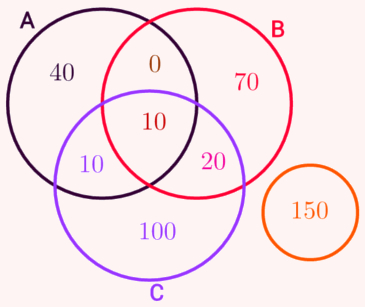






1. Diagrama de venn

3. compresión y extensión
Compresión: Los conjuntos
expresados por compresión son aquellos que expresan una característica general
del conjunto.
Ejemplos A= (x/x, son las vocales) B=
(y/y, son los días de la semana)
Extensión: Los conjuntos expresados
por extensión son aquellos que detallan todos y cada uno de los elementos del
conjunto.
Ejemplos A= (a, e, i, o, u)
B= (lunes, martes, miércoles,
jueves, viernes, sábado, domingo)
Operación de conjuntos
El conjunto de los números naturales N
Entendemos por número la expresión de un valor, la
cuantificación de una magnitud.
Los números naturales expresan valores referentes a cosas
enteras, no partidas, los números naturales van de uno en uno desde el 0, no
admiten la partición de las unidades, y solamente expresan valores positivos.
Los
números naturales son ilimitados, si a un número natural le sumamos 1,
obtenemos otro número natural.
Ejemplo: N={0, 1, 2, 3, 4, 5, 6, ... ... ...}
El
conjunto de los números enteros
Los números enteros están formados por los números
positivos, los números negativos y el cero. Los números positivos son como los
naturales, pero con un "más" delante:+1,+2,+3,+4,+5,+6,+7,+8,+9… No
obstante, el "más" de los números positivos no es obligatorio, puede
no escribirse. Por otro lado, los números negativos son como los naturales pero
con un "menos" delante:-1,-2,-3,-4,-5,-6,-7,-8,-9… El número cero es especial, porque es el
único que no tiene ni un menos ni un más delante, por esto no es ni positivo ni
negativo.
Ζ = {…-6,
-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6…}
Los números
racionales Q
Los números racionales, son el conjunto de números
fraccionarios y números enteros representados por medio de fracciones. Este
conjunto está situado en la recta real numérica pero a diferencia de los
números naturales que son consecutivos, por ejemplo a 4 le sigue 5 y a este a
su vez le sigue el 6, y los números negativos cuya consecución se da así, a -9
le sigue -8 y a este a su vez le sigue -7; los números racionales no poseen
consecución pues entre cada número racional existen infinitos números que solo
podrían ser escritos durante toda la eternidad.
Todos los números fraccionarios son números racionales, y
sirven para representar medidas. Pues a veces es más conveniente expresar un
número de esta manera que convertirlo a decimal exacto o periódico, debido a la
gran cantidad de decimales que se podrían obtener.
Q= {-3/4,5/8,31/7}
Los números
irracionales I
Números irracionales . Son los elementos de la recta real
que no pueden expresarse mediante el cociente de dos enteros y se caracterizan
por poseer infinitas cifras decimales no periódicas. De este modo, puede
definirse al número irracional como un decimal infinito no periódico.
I={ π,e, √2,√3}
Operación de conjuntos
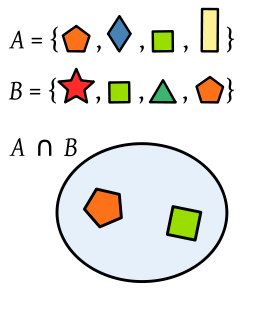
En teoría de conjuntos, la intersección de dos (o más)
conjuntos es una operación que resulta en otro conjunto que contiene los
elementos comunes a los conjuntos de partida. Por ejemplo, dado el conjunto de
los números pares P y el conjunto de los cuadrados C de números naturales, su
intersección es el conjunto de los cuadrados pares D:
P=\{2,4,6,8,10}
C=\{1,4,9,16,25}
D=\{4,16,36,64}
En otras palabras: Así, por ejemplo, si A = { a, b, c, d,
e, f} y B = { a, e, i, o, u}, entonces la intersección de dichos conjuntos
estará formada por todos los elementos que estén a la vez en los dos conjuntos,
esto es: A∩B = { a, e}
La intersección de conjuntos se denota por el símbolo ∩
por lo que D = P ∩ C.

Ejemplo:
En el diagrama de venn, los elementos de intersección de
escriben en el medio de los dos diagramas. y solo se escriben una vez.
Un ejemplo más.
B = { Luis, Inés, Ana, Beto} y N
= { Ana, Perdo, Beto}

Unión:
En la teoría de conjuntos, la unión de dos (o más) conjuntos es una operación que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales. Por ejemplo, el conjunto de los números naturales es la unión del conjunto de los números pares positivos P y el conjunto de los números impares positivos I:
P= {2, 4,6}
I= {1, 3,5}
N = {1, 2,3,4} La unión de conjuntos se denota por el símbolo ∪, de modo que por ejemplo, N = P ∪ I

Características de operacion entre conjuntos intersecion y union :

Disjuntos:

Iguales:

Unión:

Ejemplo UNION:

Símbolos utilizados en solución de conjuntos:


No hay comentarios.:
Publicar un comentario